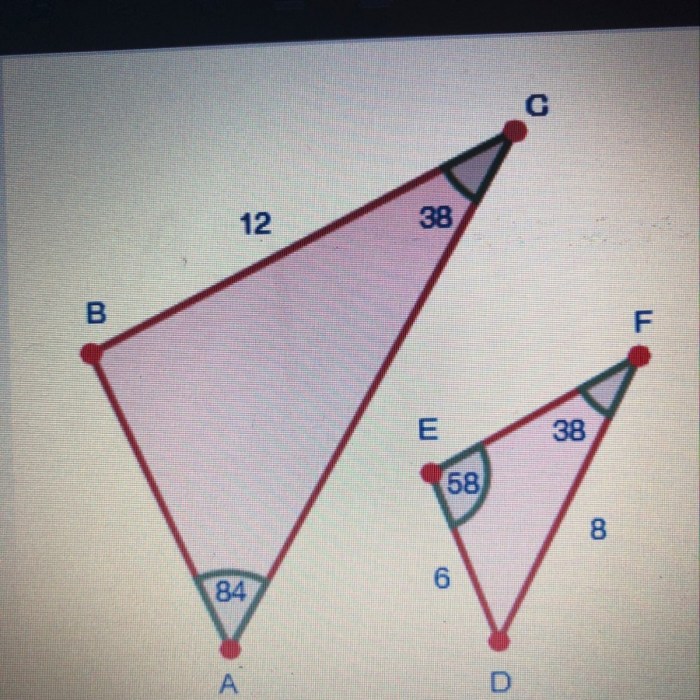
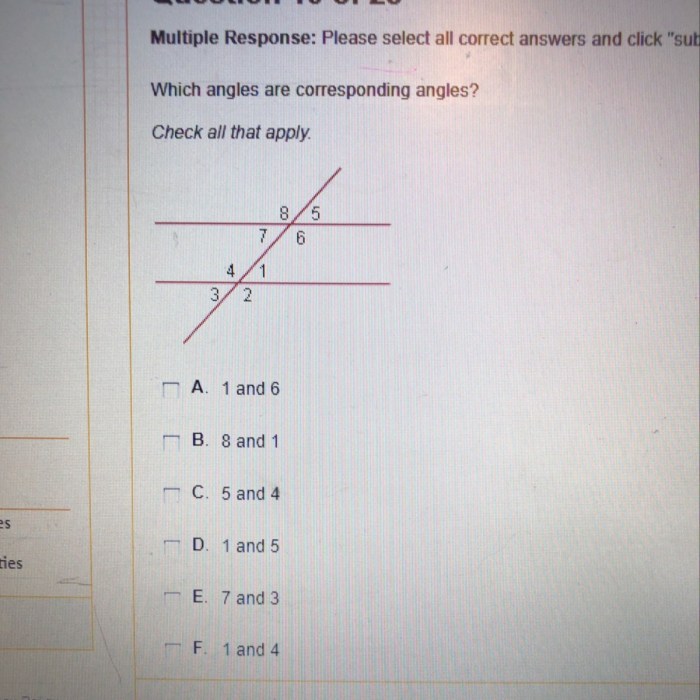
Which angles are corresponding angles check all that apply – Delving into the concept of corresponding angles, this exploration unravels their significance in the realm of geometry. Corresponding angles, as their name suggests, are pairs of angles that occupy specific positions relative to each other, forming a fundamental concept in geometric relationships.
This article aims to shed light on the intricacies of corresponding angles, exploring their properties, applications, and implications for understanding geometric figures.
Corresponding angles arise when two parallel lines are intersected by a transversal, creating four distinct angles at the points of intersection. These angles exhibit unique properties that govern their relationships, providing valuable insights into the behavior of lines and angles in geometric constructions.
Corresponding Angles: Which Angles Are Corresponding Angles Check All That Apply

Corresponding angles are angles that are formed when two lines are intersected by a transversal. They are located in the same relative position on opposite sides of the transversal.
Properties of Corresponding Angles, Which angles are corresponding angles check all that apply
The theorem relating to corresponding angles states that if two lines are intersected by a transversal, then the corresponding angles are congruent.
This theorem has several implications for angle relationships:
- If two angles are corresponding angles, then they have the same measure.
- If two angles are congruent, then they are corresponding angles.
Applications of Corresponding Angles
Corresponding angles are used in solving geometry problems involving parallel lines. For example, if you know that two lines are parallel and you know the measure of one angle, then you can use corresponding angles to find the measure of the other angles.
Corresponding angles are also used in real-life applications, such as:
- Architecture: Architects use corresponding angles to ensure that buildings are symmetrical.
- Surveying: Surveyors use corresponding angles to measure distances and angles.
- Engineering: Engineers use corresponding angles to design bridges and other structures.
Constructing Parallel Lines Using Corresponding Angles
You can use corresponding angles to construct parallel lines. To do this, follow these steps:
- Draw a line.
- Draw a transversal that intersects the line.
- Mark the corresponding angles on opposite sides of the transversal.
- Use a protractor to measure one of the corresponding angles.
- Use the protractor to draw an angle congruent to the measured angle on the other side of the transversal.
- Draw a line through the point of intersection of the transversal and the angle you just drew.
The line you just drew is parallel to the first line.
Answers to Common Questions
What are corresponding angles?
Corresponding angles are pairs of angles that occupy specific positions relative to each other when two parallel lines are intersected by a transversal.
How can corresponding angles be used to construct parallel lines?
Corresponding angles can be used to construct parallel lines by ensuring that the corresponding angles formed by the transversal and the two lines are congruent.
What are the properties of corresponding angles?
Corresponding angles are congruent, meaning they have the same measure.