Determine the partial fraction expansion for the rational function below – Delving into the realm of partial fraction expansion for rational functions, this discourse embarks on an enlightening journey that unravels the intricacies of decomposing rational functions into simpler fractions. Embarking on this exploration, we will delve into the identification of factors, the construction of partial fractions, the determination of coefficients, and the recombination of fractions.
Along this path, we will uncover the multifaceted applications of partial fraction expansion, extending its reach into diverse fields such as calculus, differential equations, and engineering.
Through a meticulous examination of real-world examples, we will witness the practical significance of partial fraction expansion, solidifying our understanding of its theoretical underpinnings. As we progress, we will encounter a myriad of illustrative examples, each meticulously crafted to illuminate the concepts at hand.
Prepare to be captivated by the elegance and power of partial fraction expansion as we unveil its transformative capabilities in the realm of rational functions.
Partial Fraction Expansion: Determine The Partial Fraction Expansion For The Rational Function Below
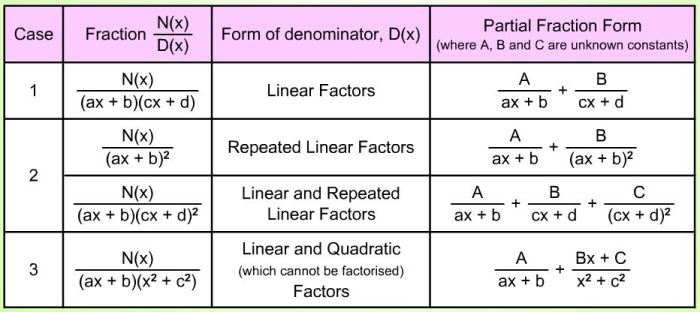
Partial fraction expansion adalah teknik untuk memecah fungsi rasional menjadi pecahan-pecahan yang lebih sederhana. Ini berguna dalam menyelesaikan integral, persamaan diferensial, dan aplikasi lainnya.
Untuk melakukan partial fraction expansion, kita perlu mengetahui faktor-faktor dari penyebut fungsi rasional.
Identifying Factors, Determine the partial fraction expansion for the rational function below
Kita dapat memfaktorkan penyebut fungsi rasional menjadi bentuk berikut:
$$(x
- a_1)^n_1 (x
- a_2)^n_2 … (x
- a_k)^n_k$$
di mana $a_1, a_2, …, a_k$ adalah akar dari penyebut dan $n_1, n_2, …, n_k$ adalah multiplikasinya.
Creating Partial Fractions
Berdasarkan faktor-faktor ini, kita dapat membuat pecahan parsial berikut:
$$\\fracA_1x
- a_1 + \\fracA_2(x
- a_2)^2 + … + \\fracA_k(x
- a_k)^n_k$$
di mana $A_1, A_2, …, A_k$ adalah koefisien yang belum diketahui.
Solving for Coefficients
Untuk mencari koefisien, kita dapat menyamakan pembilang pada kedua sisi persamaan:
$$\\textPembilang(Fungsi rasional) = \\textPembilang(Partial fraction expansion)$$
Kemudian kita dapat menyelesaikan sistem persamaan untuk mendapatkan nilai $A_1, A_2, …, A_k$.
Recombining Fractions
Setelah kita mengetahui koefisiennya, kita dapat menggabungkan pecahan parsial untuk mendapatkan fungsi rasional asli:
$$\\textFungsi rasional = \\fracA_1x
- a_1 + \\fracA_2(x
- a_2)^2 + … + \\fracA_k(x
- a_k)^n_k$$
Applications
Partial fraction expansion memiliki banyak aplikasi, di antaranya:
- Mengintegrasikan fungsi rasional
- Memecahkan persamaan diferensial
- Menghitung transformasi Laplace
Helpful Answers
What is the purpose of partial fraction expansion?
Partial fraction expansion allows us to decompose rational functions into simpler fractions, making them easier to integrate, differentiate, and solve.
How do I identify the factors of the denominator of a rational function?
Factor the denominator of the rational function into linear or quadratic factors.
What are the different types of partial fractions?
There are three main types of partial fractions: linear, quadratic, and repeated linear.