Embark on a captivating journey with the Parent Functions Graphic Organizer Answer Key, a comprehensive guide that unravels the mysteries of parent functions and their transformations. This invaluable resource empowers you to decipher the intricacies of graphical representations, enabling you to navigate the world of functions with confidence.
Prepare to delve into a world of mathematical transformations, where parent functions serve as the foundation for a myriad of graphical marvels. Our comprehensive guide will equip you with the knowledge and tools to identify, manipulate, and apply parent functions, unlocking their potential for modeling real-world phenomena.
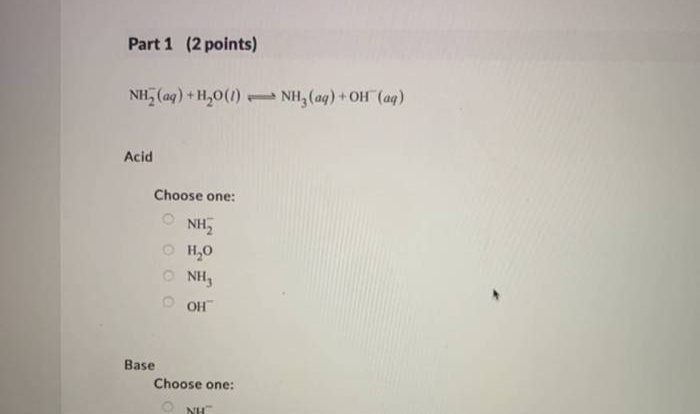
Parent Functions and Their Graphs

Parent functions are the basic functions that form the foundation for more complex functions. They have simple equations and distinct graphs that serve as building blocks for transformations and other operations.
Common parent functions include:
| Function | Equation | Graph |
|---|---|---|
| Constant function | f(x) = c | Horizontal line at y = c |
| Linear function | f(x) = mx + b | Straight line with slope m and y-intercept b |
| Quadratic function | f(x) = ax2 + bx + c | Parabola opening up (a > 0) or down (a < 0) |
| Absolute value function | f(x) = |x| | V-shaped graph with a vertex at the origin |
| Square root function | f(x) = √x | Right half of a parabola opening up |
| Exponential function | f(x) = ax | Exponential curve increasing (a > 1) or decreasing (0 < a < 1) |
| Logarithmic function | f(x) = loga(x) | Inverse of the exponential function |
Transformations of Parent Functions: Parent Functions Graphic Organizer Answer Key
Transformations are operations that can be applied to parent functions to create new functions with different graphs. Common transformations include:
| Transformation | Effect on Graph |
|---|---|
| Vertical shift | Moves the graph up (positive shift) or down (negative shift) |
| Horizontal shift | Moves the graph to the right (positive shift) or left (negative shift) |
| Vertical stretch | Stretches the graph vertically by a factor of |a| |
| Vertical shrink | Shrinks the graph vertically by a factor of |a| |
| Horizontal stretch | Stretches the graph horizontally by a factor of |a| |
| Horizontal shrink | Shrinks the graph horizontally by a factor of |a| |
| Reflection | Reflects the graph over the x-axis (y-reflection) or y-axis (x-reflection) |
Identifying Parent Functions
Identifying the parent function of a given graph involves:
- Examining the shape and key features of the graph
- Matching the shape to the corresponding parent function
- Considering the transformations applied to the parent function
Tips for identifying parent functions:
- Look for symmetry and vertex form for quadratic functions
- Check for the presence of asymptotes for exponential and logarithmic functions
- Consider the range of the function to identify absolute value functions
Applications of Parent Functions
Parent functions are widely used in various fields, including:
- Mathematics:Modeling curves, surfaces, and other mathematical objects
- Physics:Describing motion, growth, and decay
- Economics:Analyzing market trends and consumer behavior
- Biology:Modeling population growth and enzyme reactions
- Computer science:Designing algorithms and analyzing data
FAQ Guide
What are the key characteristics of parent functions?
Parent functions exhibit distinct characteristics, including a well-defined shape, a specific equation, and a predictable behavior under transformations.
How can I identify the parent function of a given graph?
To identify the parent function, analyze the graph’s shape, symmetry, and intercepts. Compare these features to the characteristics of common parent functions.
What are the different types of transformations that can be applied to parent functions?
Parent functions can undergo various transformations, including translations, reflections, stretches, and compressions, which alter their position, orientation, and shape.